Isotropic loss of free-space radiation

Introduction

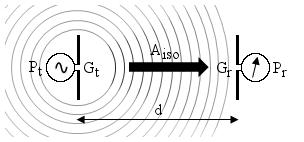
If we have two antennas at some distance apart, one connected to a transmitter and the other one connected to a receiver, it can be very interesting to know how much power radiated by the first antenna will be picked up by the second one. Transmitter power, and both antenna gains are usually well known; the question is how much is it lost in the air.

The above diagram summarizes the problem: a transmitter is delivering the power P_t to a transmitting antenna of gain G_t. At a distance d there is a receiving antenna of gain G_r that delivers the power P_r to a receiver. In this page we determine A_iso, that is the loss introduced by the distance the waves have to travel.

Some theory

This can be modeled as a spherical wave leaving the transmitting antenna and increasing its radius as it travels away. Somehow in a very similar way as circular ripples spreads out when a stone is dropped in a pond. The power that was initially spread on a very small spherical surface, will be distributed on a larger and larger surface as the sphere gets bigger and bigger. This is called geometrical attenuation, or isotropic loss of free space radiation or sometimes simply path loss.

The surface of the wave increases with the square of the radius (the distance d) and the further we are from the source, the smaller power the density we get. Since the same power is spread on a greater surface, the geometrical loss also increases with the square of the distance. This loss is only a function of the distance (in terms of wavelength). It doesn't depend on the gain of the antennas; of course, using antennas with a higher gain will increase the signal, but the geometrical loss will still be the same.

The isotropic loss a_iso can be determined with the following equation:

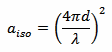
Now, a_iso is just a dimensionless number between 0 and 1. It's much more practical to convert it in dB and get A_iso with the following formula:

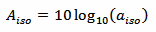
Just by looking at the a_iso formula, one may conclude that, since lower frequencies have less path loss, using high frequencies is a bad idea... Well, this isn't true: the a_iso formula is not the whole picture! Actually, high frequencies are more interesting because it's much easier to build high gain antennas. This largely compensates and overcomes the additional path loss. So, for a given radio link; distance, antenna orientation and antenna size being equal, a higher frequency will provide more power to the receiver, even if the path loss, alone, is higher.

This calculator doesn't take into account the gain of the antennas and the transmitted power, it just calculates the losses due to the distance. In order to calculate the received power P_r (in dBm), one has to consider the transmitter power P_t (in dBm), add the gain of the transmitting antenna G_t (in dBi), remove the path loss A_iso (in dB) found with this tool and add the gain of the receiving antenna G_r (in dBi). Additional cables losses or absorption in materials (such as moist air) can also be subtracted. The basic idea, when dealing with dB, is to add all the gains to the transmit power and subtract all the losses to find the received power.

Loss in the air can usually be neglected below a few dozens of GHz, it may become a big problem at, say, 50 GHz, but this is outside the scope of this page.

As usual, this model is only valid if each antenna is in the far field region of the other one. This is not a big limitation, since antennas are usually intended to cover large distances, much bigger than their physical dimensions or than the selected wavelength.

Then, of course, in order to really get the calculated signal out of the receiving antenna, a few other considerations may be worth mentioning: for example, the space between the two antennas must be free (both antenna must be in line of sight), both antennas must have the same polarization and must be aligned to aim to each other. The impedance of the transmitter must match the one of its cable, and the cable must match its antenna. The same is true for the receiver side.

Isotropic loss calculator

Enter the frequency f and one value (either d or A_iso), then click the "Calculate" button next to it to compute the other one.

An example

In the picture below, we see two antennas about 50 m apart. Let's suppose the GSM site transmits at a frequency f = 1'820 MHz. With the calculator we find an isotropic loss of A_iso = 72 dB.

If we want to know the power that the log-periodic antenna in the foreground will deliver to a receiver, let's now make some more assumptions: we suppose that the GSM site is equipped with a 20 W (+43 dBm) transmitter, that it has 3 dB loss in the cable and that its antenna has a gain of 18 dBi. We suppose also that the receiving log-periodic antenna has a gain of 5 dBi and that there are 2 dB of cable loss.

The power delivered to the receiver will be: +43 dBm – 3 dB + 18 dBi – 72 dB + 5 dBi – 2 dB = –11 dBm that mean 79 μW.

One may remark that the receiving antenna is horizontally polarized, while GSM base antennas usually have 45° polarization. So, if the receiving antenna stays horizontal, about 3 additional dB are lost because of the wrong polarization, bringing the received power down to –14 dBm or 40 μW. Of course, the receiving antenna should be tilted at 45° to get the maximum signal, but this didn't look that nice on the picture...

Bibliography and further reading