Calculating mains frequency power transformers

In this page a simple method of calculating mains frequency closed core power transformers. This is intended for home brewing, repairing and modifying transformers. Please remark that even if the method and some equations could be generalized, only classical cores composed by steel plates are taken into account.

Simplified drawing of a typical transformer

The size of the core

When designing a closed core power supply transformer, the first step is to choose a suitable core according to the power the device will have to handle. Usually, for high power, large cores are required. Actually, there is no theoretical physical reason preventing a small core to handle a large power, but for practical reasons, on a small core there is not enough space to fit the windings and a larger core is the only choice. In order to choose a pretty good core right form the beginning, the following empirical formula (for a working frequency of 50 Hz) can help:

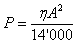
P = eta * A^2 / 14000

This equation links the (apparent) power P to the core cross-section surface A, taking into account core efficiency η (Greek "eta"). When measuring the core cross-section, one should remove about 5% in order to take into account the varnish on the ferromagnetic plates composing the core. The cross-section is the minimum cross-section of the magnetic circuit, usually measured where the windings are located as shown in the drawing below.

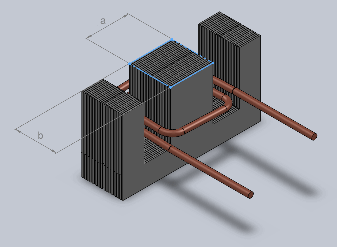
Typical transformer cut view shoqing the effective cross-section a*b

The efficiency depends on the material composing the core; if not known, the table below will give a rough idea.

Core plate material Flux density φ
[Wb/m2]		 Efficiency η
[1]
Grain-oriented silicon steel (C-shaped), M5 1.3 0.88
Grain-oriented silicon steel (0.35 mm plates), M6 1.2 0.84
Non grain-oriented silicon medium steel (0.5 mm plates), M7 1.1 0.82
Non grain-oriented silicon standard steel (or for heavy duty) 1.0 0.80
Mild steel 0.8 0.70

In order to simplify this operation the following calculator can be handy:

Core power: P =   VA
Core surface: A =   mm2
Core efficiency: η =   

This calculator already takes into account the 5% reduction of the core cross section.

Flux density in the core

Then, one has to determine the core flux density φ (Greek "phi"). Again, this depends on the material and, if not known, the same table will help. If the transformer is supposed to run continuously or in a poorly ventilated environment, reducing slightly the flux density (by 10%, for example) will reduce losses and keep the transformer cool at the cost of more iron and more copper. The opposite can be considered for reducing material cost in transformers only used for short periods of time.

Once the flux density has been determined, one can calculate the number of turns per volt of the windings, with the following formula:

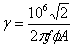
gamma = 1E6 * sqrt(2) / (2 * pi * f * phi * A)

The 106 factor takes into account that the core cross section is expressed in mm2. A few things should be remarked by looking at this formula: first is that lower frequencies require more turns as one may have remarked by looking at 60 Hz transformers that are usually a little smaller than equivalent 50 Hz ones. Than that a lower flux density also requires more turns, meaning that to lower the flux in the core (and reduce losses) one have to wind more turns. The final remark is that large cores require few turns.

Calculating the windings

Now that we know how many turns per volt our windings require, it's easy to calculate the number of turns for each winding with the formula:

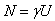
N = gamma * U

Please remark that all voltages and currents are RMS values, while the flux density is expressed in its peak value to avoid saturation, and this explains the √2 term in the equation of the turns per volt.

For secondary windings, it's a good practice to increase slightly the number of turns, say by 5% to compensate losses in the transformer.

In order to simplify this operation the following calculator can be handy:

Working frequency: f =   Hz
Core surface: A =   mm2
Flux density: φ = 
Primary voltage: Up =   V
Secondary voltage: Us =   V
Transformer ratio: ü =   : 1
Transformer constant: γ =   turns/V
Primary turns: Np =   turns
Secondary turns: Ns =   turns

This calculator already takes into account the 5% factor for the secondary turns.

Choosing the right wire

The final step is to calculate the diameter of the wire of each winding. To do this a conductor current density c has to be chosen. A good compromise is 2.5 A/mm2, a lower value will require more copper and generate fewer losses and is suitable for heavy duty transformers, while a higher value will require less copper making the transformer cheaper but because of the increased heat, it will only be acceptable if used for short periods of time. Common values are between 2 and 3 A/mm2. Once the current density is determined, the wire diameter can be calculated using the following equation:

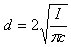
d = 2 * sqrt( I / (pi * c) )

Or, for c = 2.5 A/mm2:

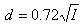
d = 0.72 * sqrt(I)

In order to simplify this operation the following calculator can be handy:

Wire current: I =   A
Wire diameter: d =   mm
Wire cross section: S =   mm2
Current density: c =   A/mm2  

In practice

Now the calculations are terminated and the hard part begins: will the calculated windings fit on the core? Well, the answer is not easy and depends on a large number of factors: wire cross-section and shape, wire bending radius, quality of the winding, presence or not of insulating foils between winding layers, and so on. On the other hand, some experience will be more helpful than plenty of equations.

It's hard buy an empty transformer core, and usually home projects start from and old transformer to unwind and rebuild. Not all transformers can be disassembled: some are glued together with a resin that is too strong to remove without bending the core plates. Fortunately many transformers can be disassembled by removing the cover that holds all the plates together or by sawing in the two welding across all plates. Than, every plate has to be carefully removed in order to get access to the windings.

A disassembled transformer

With some luck one can reuse the primary winding and rebuild only the secondary, unless the primary is winded over the secondary or has an unsuitable number of turns. When deciding a winding should be kept as is or not, it's useful to determine its number of turns. To do this, before disassembling the core, just wind a few turns (say 5 or so) of wire around the winding and measure the voltage induced when powering the transformer normally. Form this is easy to calculate the turns per Volt of the transformer and calculate the number of turns of every winding without actually counting them.

After new windings have been winded, it's time to rebuild the core, by putting all the plates back in place. Without a power press it will be hard to put back all of them, but if at the end one or two plates are left, the transformer will work fine anyway, but for this reason, one should slightly oversize the transformer when doing the calculations and select a smaller core cross-section. When the transformer is powered, the force on the core plates is significant and it's important to hold them tightly or to glue them, otherwise the core will vibrate and will be very noisy.

Correct way of assembling E-I cores

Many transformers have E-I core plates, like the one in the above picture. When rebuilding the core, the plates have to be crossed: E-I for one layer and I-E for the following one, and so on. This minimizes the air gap and helps keeping the coupling factor high.

Used symbols

Symbol Description Unit
A Core cross-section mm2
d Wire diameter mm
f Working frequency Hz
I Winding RMS current A
N Number of turns 1/1
P Pransformer apparent power VA
U Winding RMS voltage V
γ Number of turns per V turns/V
η Core efficiency 1/1
φ Core magnetic flux density Wb/m2

Remark: 1 Wb/m2 = 1 T = 10'000 Gauss

Bibliography

Home Electronics 008352 Last update: 12/13/11