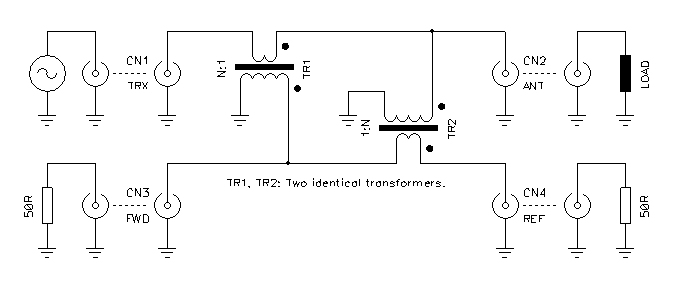
Circuit diagram of the tandem match coupler.
When you're trying to match and antenna (or a load) to a transmission line, you need some sort of circuit capable of measuring the forward and the reflected power. I've used the tandem match to measure forward and reflected power on many transmitter and antenna matching projects, mainly because it's simple to build and works very well. Even if the circuit looks really simple (only two transformers) the way it works is, in my opinion, not self explanatory and deserves some explanations. I wasn't able to find any detailed technical description in the literature I have, so I decided to spend some time in analyzing it and to write this page.
The "tandem match coupler" or "Sontheimer bridge" is a very interesting and tricky circuit. It was invented by C. G. Sontheimer in 1966 (patent number US 3,426,298) and derives directly from the telephone hybrid that was known long before. It's more a directional coupler than an impedance bridge.
In order to understand how this coupler works a few concepts must be made clear first. When a transmission line is terminated on an impedance different from its characteristic one, on top of the forward wave travelling from the generator to the load, a reflected wave travels in the opposite direction. The superposition of these two waves is called a standing wave. Because of this standing wave, measured voltage and current are not constant along the line and the figures depend on where on the line the measurements are taken. This is, of course, only an effect of the superposition of forward and reflected waves which, if taken alone, would show the same voltage and current at any point in the line.
What allows the coupler to separate these superposed waves, is the fact that the current of the reflected wave is 180° out of phase compared to the current of the forward wave. In other words, when the voltage is positive and the wave is travelling toward the load, the current is, say, positive (flowing from left to right). For the reflected wave travelling from the load toward the generator, a positive voltage will be accompanied by a current travelling the other (negative) direction (flowing from right to left), explaining the 180° phase shift.
It's interesting to remark that the voltage and the current of a travelling wave in a line are always in phase. Since the wave is travelling along the line, it has no idea of what kind of impedance it will find at the end, so the relation between voltage and current is determined only by the characteristic impedance of the line, which is a real number, ensuring 0° phase shift. The same is true for the reflected wave going in the other direction: again voltage and current are in phase, but because of the opposite direction, we say that there is a 180° phase shift as explained above. Now, when the forward wave reaches the end of the line and is reflected, the reflection phase shift depends on the termination impedance which may be reactive and can therefore reflect part of the wave with a phase shift. This phase shift will of course determine the position of maxima and minima of the standing wave and will also change the impedance seen by the generator, but voltage and current of forward and reflected waves taken alone are always in phase.
In order to measure the power on a real load, one can simply measure the voltage on a known real impedance Z and simply use the formula P = U2/Z or measure the current flowing through Z and use the formula P = ZI2.
Unfortunately this can only be done on the line if there is no standing wave, otherwise voltage and current vary along the line and measurements will be wrong. In order to measure the power at any point along the line when a standing wave is present, one need a special circuit able to separate the forward from the reflected wave, such as the tandem match coupler described here.
The trick is to determine the power by calculating part of the power based on the measured current and part based on the measured voltage; than add them together. Since the current of the reflected wave is 180° out of phase compared to the forward wave, the circuit is arranged in such a way that at one port the voltage and current (over a resistor) cancel for the forward wave and add together for the reflected wave and that at another port we have the opposite situation.

Circuit diagram of the tandem match coupler.
The coupler is composed by two transformers. The first one, TR1, is used as a current transformer and takes a sample of the main current while the second one, TR2, is used as a voltage transformer and takes a sample of the voltage. Since the transformers are identical the current and the voltage are reduced by the same ratio, keeping the impedance constant. The circuit is perfectly symmetrical and all ports have the same impedance.
By the way, the impedance is not directly determined by this coupler, which doesn't have any fixed resistor or impedance value. The working impedance is only determined by the characteristic impedance of the line connected to CN1 and CN2 and by the two load impedances connected to CN3 and CN4 that must have the same value as the line impedance (50 Ω, for example).
The two transformers are connected in such a way that for a wave travelling from CN1 to CN2, signals adds up on CN3 and cancel on CN4, and for a wave travelling from CN2 to CN1, signals cancel on CN3 and adds up on CN4.
To better understand how this circuit works, let's deal separately with the forward and with the reflected wave. Since everything is linear, the superposition principle applies, meaning that we can consider the two cases alone and than add them together if we have a standing wave (a superposition of forward and reflected wave). Because of the same superposition principle, we can also treat separately the induced current by TR1 and the induced voltage by TR2 and than add them together. This dramatically reduces the complexity of this problem.
Let's suppose that at a given time the voltage Uline on the main line is positive and a current Iline is flowing from CN1 (the generator) to CN2 (the load) as shown in the figure below. Let's also suppose that two identical real impedances Z are connected to CN3 and CN4 and that these impedances have the same value of the line impedance Z.
Please remark that with the notation used here, a positive voltage is represented by an arrow pointing in the same direction as the electrical field: from "+" to "–". A positive current is also represented with an arrow flowing from "+" to "–". For clarity, currents are drawn in red and voltages in blue.
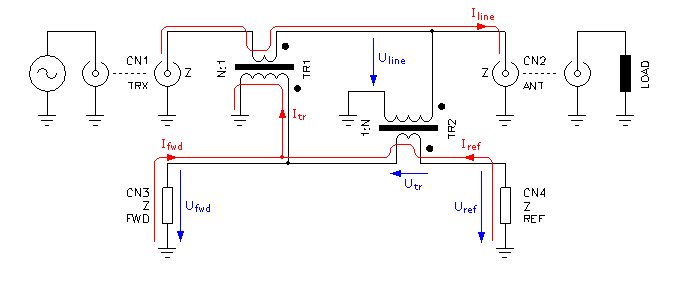
Circuit diagram of the tandem match coupler showing voltage and current of the forward wave.
Let's consider the voltage first: TR2 works as a voltage transformer stepping down the line voltage Uline by a factor N, N being is the transformer ratio. On its secondary (the winding with less turns) we have therefore:
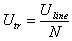
Since the two loads on CN3 and CN4 appears connected in series and are identical, each one gets half of this induced voltage but with opposite polarity:
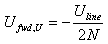
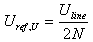
These voltages, noted Ufwd,U and Uref,U represent the contribution of the voltage transformer to the voltage on CN3 and CN4. They are not the total voltage on these ports, since we still have to add the contribution of the current transformer.
Now, let's have a look at the current: TR1 works as a current transformer inducing on its secondary (the winding with more turns) a current N times smaller than the main line current Iline and we have:
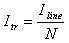
We have seen before that if we only consider the forward or the reflected wave alone, wave voltage and wave current are in phase, and their relation is controlled by the line impedance Z. We can therefore write:
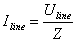
Putting this in the previous equation, we have:
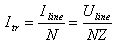
The direction of the currents is indicated in the diagram. Both CN3 and CN4 have the same impedance Z and appear in parallel, each one receiving half of the current. We can now calculate the current that will flow in the ports CN3 and CN4 due to the current transformer. Again, this is not the total current on these loads.
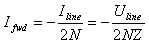
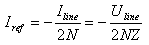
Or, in terms of voltages, we can now calculate the contribution of the current transformer on CN3 and CN4, that we write as Ufwd,I and Uref,I:
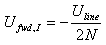
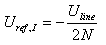
If now we superpose the effects of the current and of the voltage transformer, we see that at CN3 we have:
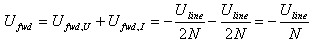
And that at CN4 we have:
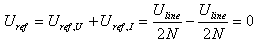
In other words, when a wave travels from CN1 to CN2, no voltage appears on CN4 and a voltage stepped down N times appears on CN3. The minus sign tells us that the voltage on CN3 is 180° out of phase from the line voltage.
It has been said before that TR1 works as a current transformer stepping down the line current N times. Of course, half of this current flows through the secondary of TR2 which further transforms it back to the main line. This stray current path is not shown on the diagram. Since TR2 acts in this situation as another step-down current transformer, the current is again divided by N and can be neglected (N is normally a large number in the 10 to 50 range). The same is true for the voltage transformed by TR2 and induced back by TR1.
If we look now at the reflected wave, the voltage has still the same sign, but the current flows in the opposite direction, as shown in the figure below:
Circuit diagram of the tandem match coupler showing voltage and current of the reflected wave
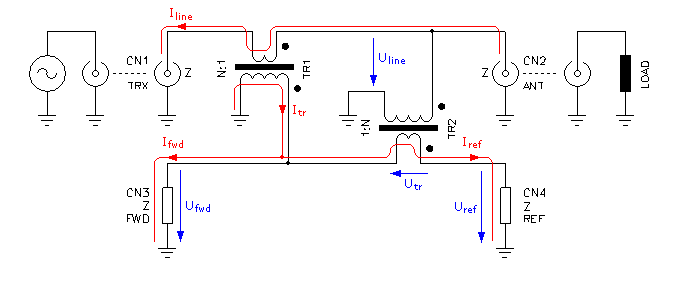
We can go through the same procedure again and find that this time we have at CN3:
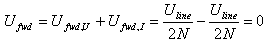
And at CN4:
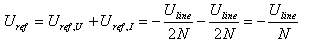
In other words, when a wave travels from CN2 to CN1, no voltage appears on CN3 and a voltage stepped down N times appears on CN4. Again, the minus sign tells us that this signal is 180° out of phase.
If we have a standing wave, both forward and reflected waves are present at the same time. Since this circuit is linear, the two situations explained above superpose simultaneously and on CN3 we have a voltage which is an N fraction of the forward wave voltage and on CN4 we have the same for the reflected wave.
This coupler is very popular for frequencies ranging from a few kHz roughly up to 100..200 MHz. When used on high frequencies and with a wide frequency range, it's a good idea to use shielded transformers to kill any stray capacitance between the primary and the secondary windings. Since one winding usually has only one turn, it's common practice to use a shielded cable with the shielding grounded at only one end. In this case it's very important not to ground the other end, otherwise the transformer will have a shorted winding!
Stray coupling between transformers should be minimized, by using toroidal transformers, by putting a metal screen in-between or both.
One also has to make sure the impedance of the transformer winding (with more turns) is much larger than the desired line impedance (this sets the lower frequency limit) and that the self resonance of the same winding is high enough (this sets the higher frequency limit).
Since linearity is mandatory, one has to make sure that both transformers are not saturating and that their cores have very little hysteresis losses. For this, a wise core selection in terms of material and cross-section is a must.
The tandem match is common and widely used directional coupler. In this document its basic working principle has been described, explaining how the forward wave can be distinguished from the reflected wave in a line with a standing wave. Despite its simplicity, the way this coupler works is not evident at first sight and I hope this document may be of some help.
| Home | Electronics | Page hits: 051388 | Created: 08.2013 | Last update: 08.2013 |